|
ESTER
Evolution STEllaire en Rotation
|
|
ESTER
Evolution STEllaire en Rotation
|
The diff_gl class implements the Gauss-Lobatto (or more properly Gauss-Lobatto-Chebyshev) collocation method. More...
#include <numdiff.h>
Public Member Functions | |
| diff_gl (int n=1) | |
| ~diff_gl () | |
| diff_gl (const diff_gl &) | |
| diff_gl & | operator= (const diff_gl &) |
| void | set_ndomains (int n) |
| void | set_xif (double,...) |
| void | set_npts (int,...) |
| void | init () |
| matrix | eval (const matrix &y, const matrix &x, matrix &T) const |
| matrix | eval (const matrix &y, const matrix &x) const |
| matrix | eval (const matrix &y, double x) const |
| matrix | eval (const matrix &y, double x, matrix &T) const |
Public Attributes | |
| matrix | x |
| matrix | I |
| matrix_block_diag | P |
| matrix_block_diag | P1 |
| matrix_block_diag | D |
| int * | npts |
| double * | xif |
| const int & | ndomains |
| const int & | N |
Private Member Functions | |
| void | init_1 () |
Private Attributes | |
| int | ndom |
| int | Ntot |
The diff_gl class implements the Gauss-Lobatto (or more properly Gauss-Lobatto-Chebyshev) collocation method.
The basis functions are Chebyshev polynomials of the first kind: \( T_l(x)=cos(l.arccos(x)) \), defined in \( [-1, 1] \).
And the collocation points are \( x_i = -cos(\frac{i \pi}{n})\)
|
explicit |
| diff_gl::~diff_gl | ( | ) |
| diff_gl::diff_gl | ( | const diff_gl & | gl | ) |
| void diff_gl::init | ( | ) |
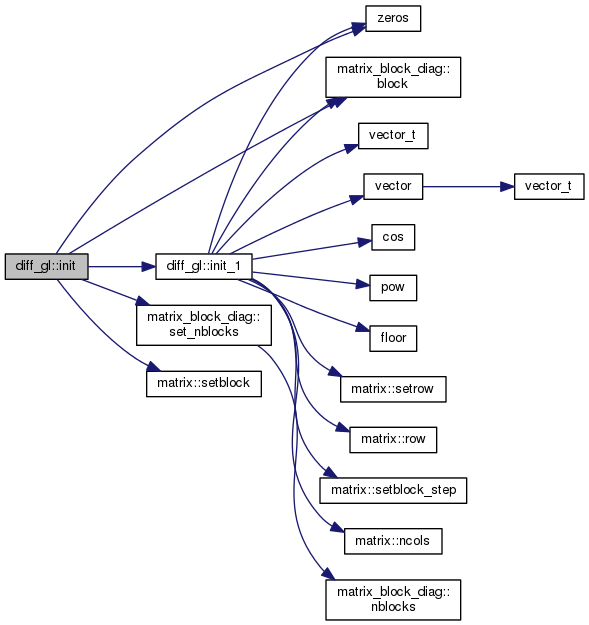
|
private |
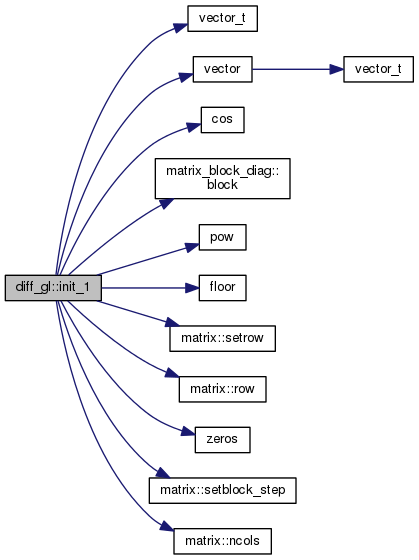
| void diff_gl::set_ndomains | ( | int | n | ) |
| void diff_gl::set_npts | ( | int | n, |
| ... | |||
| ) |
| void diff_gl::set_xif | ( | double | x, |
| ... | |||
| ) |
| matrix_block_diag diff_gl::D |
| matrix diff_gl::I |
| const int & diff_gl::N |
|
private |
| const int& diff_gl::ndomains |
| int* diff_gl::npts |
|
private |
| matrix_block_diag diff_gl::P |
| matrix_block_diag diff_gl::P1 |
| matrix diff_gl::x |
| double* diff_gl::xif |
 1.8.6
1.8.6